Electrochemistry
Conductivity
of electrolytes
The substance which allows the flow of
electricity through them are called conductors. We all are very familiar with
resistance. Resistance is that property of material due to which it opposes the
flow of electrons (in case of electric circuit). One term that is associated
with resistance is resistivity. Resistivity is a property that describes the
extent to which a material opposes the flow of electric current through it.
Similarly, conductance is also a property of any substance which acts opposite
to that of resistance. As we know, the flow of electricity involves the flow of
electrons. Therefore, we can say that transfer of electrons takes place in
conductive materials. On the basis of the mechanism of transfer of electrons,
conductors are classified as electronic and electrolytic conductors.
Electronic
Conductors: The conductors in which the conduction of
electricity takes place by a direct flow of electrons under the influence of
applied potential are called electronic conductors. For example, solid and
molten metals like Copper, Aluminium, etc.
Electrolytic
Conductors: The conductors in which the conduction
takes place by the migration of positive and negative ions are called
electrolytic conductors. For example, solutions of ionic solids, strong and weak
acids and bases.
Factors
that affect conductivity of electrolytes
Concentration
of ions
The only
reason for the conductivity of electrolytes is the ions present in them. The
conductivity of electrolytes increases with an increase in the concentration of
ions. Ions acts as charge carriers.
Nature
of electrolyte
Electrolytic
conduction is significantly affected by the nature of electrolytes. The degree
of dissociation of electrolytes determines the concentration of ions in the
solution and hence the conductivity of electrolytes.
Temperature
Temperature
affects the degree to which an electrolyte gets dissolved in a solution. Higher
temperature enhances the solubility of electrolytes and hence the concentration
of ions which results in increased electrolytic conductance.
The nature of
solution can be determined by measuring their conductivities. The substance
whose aqueous solution conduct electricity are called electrolytes whereas
those whose aqueous solution conduct the electricity to a very small extent or
negligible are called non-electrolytes. Sodium Chloride, Potassium Chloride,
Acetic acid are examples of electrolytes. Urea and glucose are examples of
non-electrolytes. Electrolytes are further classified as
Strong
electrolytes: The substance that are
almost completely ionized in aqueous solutions are called strong electrolytes.
Example: Strong acids, strong bases, ionic salts.
Weak
electrolytes: The substance that are
ionized to a very small extent in aqueous solutions are weak electrolytes.
Example: Weak acids and weak bases
The
conductivity of aqueous solution of strong electrolytes is greater than that of
aqueous solution of weak electrolytes with the same concentration.
Ohm’s law
Ohm’s law states that “When physical state
(length, material, area and temperature) of a metallic conductor remains
constant, the electric current through that conductor is directly proportional
to the potential difference across the ends of a conductor”.
Experimental verification of
Ohm’s law
Consider the
given diagram. The circuit consists of a battery and a metallic conductor. The
potential difference applied across the end of the conductor is V. The current
flowing through the circuit is I. It can be seen that as voltage V across the
conductor increases, current flowing through the circuit also increases.
|
Voltage
|
Current
|
|
5V
|
0.1A
|
|
6V
|
0.3A
|
|
7V
|
0.4A
|
|
8V
|
0.5A
|
|
9V
|
0.55A
|
As we can see
from the data obtained, that for each increased potential difference, the
current flowing through conductor increases. The graph plotted from above table
is given below
Thus, we can
say that
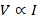
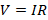
Where, R is
constant of proportionality and is known as resistance. Resistance in a conductor
opposes the flow of current through it.
Factors
affecting resistance
Cross
sectional area: Resistance of a conductor is inversely proportional to its
cross-sectional area. Resistance decreases with increase in cross sectional
area.
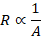
Length
of the conductor: Resistance of a conductor is directly
proportional to its length. Resistance increases with increase in length of the
conductor
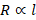
Material:
Resistance
also depends on the material of the conductor.
Temperature: Resistance
is inversely proportional to temperature. It decreases with increase in
temperature.
Specific
resistance
The
resistance R of a conductor is
–
directly
proportional to its length
–
inversely
proportional to its area of cross-section
Hence,
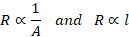
i.e.
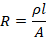
Where, p
is constant of proportionality and is known as resistivity or specific
resistance. Specific resistance is defined as the resistance of uniform column
of the material of the conductor having a length of 1 cm and a cross section of
1cm2. It is denoted by symbol rho (p) and its unit is Ohm.cm
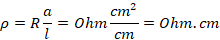
Specific conductance
The specific
conductance of a conductor is defined as the reciprocal of specific resistance.
It is defined as the ability of a conductor to conduct electricity. It is
denoted by symbol kappa (
) and its unit Ohm–1cm–1
or mhos/cm. Specific conductance is defined as the conducting capacity of a
solution of the dissolved electrolytes and the whole solution is being placed
between two parallel electrodes which are 1 cm distance apart and have a 1cm2
area of cross section. In other words, it is the conductance offered by 1cm3
of a solution.
Hence,
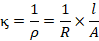
The greater
the specific conductance, the electrolyte conducts more electricity.
Equivalent
conductivity
When one gram
equivalent of an electrolyte is dissolved in a solution then conducting power
of all the ions produced is called equivalent conductivity. Therefore, it can
be defined as conductivity of a solution containing one gram equivalent of
electrolyte placed between two sufficiently large electrodes of cross-sectional
area of 1cm2 separated by a distance of 1 cm. It is denoted by
symbol lambda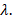 
Hence,
Vol. (in cm3
containing 1 gm equivalent x specific conductivity of solution
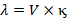
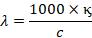
Where, c is
the concentration in gm equivalent per litre.
Molar
conductance
Molar
conductivity is the conductance of a solution containing one mole of
electrolyte placed between two electrodes of unit cross-sectional area. In
other words, molar conductivity is the total conducting power of all the ions
generated when a mole of electrolytes is dissolved in a solution. George
Kohlrausch introduced the concept of molar conductivity to determine the
electrolyte’s efficiency to conduct electricity in a solution. It is denoted by
the symbol caret 
. Mathematically it is
defined as
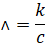
Where,
k
is the specific conductivity
c
is the mole per litre concentration
Variation
of specific conductance with dilution
As we know,
specific conductance depends on the number of ions per unit volume of solution.
On increasing the dilution or on decreasing the concentration, the number of
ions per unit volume decreases so that the specific conductance of an
electrolytic solution goes on decreasing with dilution. As strong electrolytes
are completely ionized in the solution with increase in concentration, the number
of ions per volume of the solution increases, hence the specific conductivity
increases. In case of weak electrolytes, there is partial dissociation due to
which increase in number of ions per unit volume with concentration is
comparatively small, therefore, conductivity does not increase rapidly as in
strong electrolytes.
Variation
of molar conductance with dilution
The molar
conductivity is the conductivity is the conductance of all the ions produced by
one mole of electrolyte. The molar conductance of an electrolytic solution
depends on the number of ions and the mobility of ions. On dilution, the total
number of ions increases due to increase in degree of dissociation. Hence, the
molar conductance of both weak, as well as strong electrolytes, increases on
increasing dilution or decreasing the concentration. On dilution, the molar
conductivity of strong electrolytes increases up to the maximum limiting value 
i.e. value at zero
concentration or at 
dilution. The molar
conductivity reaches the vale in just 0.001 or 0.0001
M solutions of strong electrolytes but for weak electrolytes at these
concentrations it is less than .
Variation
of equivalent conductance with dilution
The
equivalent conductance of an electrolytic solution depends on the number of
ions and the mobility of ions i.e the speed with which the ions move. On
dilution, the number of ions as well as the speed of ions increases. The number
of ions increases due to an increase in the degree of ionization and the
mobility(speed) of ions increases due to a decrease in interionic attraction
between oppositely charged ions on dilution. Therefore, the equivalent
conductance increases on dilution.
In the case
of weak electrolytes, the degree of ionization increases, and interionic force
decreases on dilution so that the number of ions and speed of ions increases
which results in an increase in equivalent conductance.
Similarly, In
the case of strong electrolytes, the number of ions is the same at all
dilutions. The increase in equivalent conductance is mainly due to an increase
in the speed of ions with dilution. As dilution is increased, the interionic
forces decrease as a result, the speed of ions increases.
Friedrich
Kohlrausch gave the relation
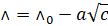
Where, a is a
constant and is molar conductivity
at dilution. The graph of of strong and weak
electrolytes vs concentration is given above.
The degree of
dissociation of weak electrolytes is related to its molar conductivity at
concentration C by an equation
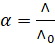
Where,
Molar conductivity at
zero concentration
Molar conductivity at
concentration C
The
dissociation constant k of weak electrolyte is given by
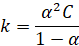
Substituting
the value of 
, we have
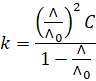
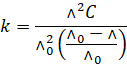
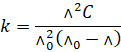
Cell
constant
The cell
constant is defined by the distance between the electrodes (l) and their
cross-sectional area (A). The conductivity, k of an electrolytic solution is
given by
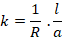
The ratio 
is known as
cell constant and is denoted by ‘b’.
Therefore,
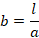
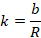
The unit of
cell constant is m–1 or cm–1
Determination
of cell constant
To determine
the cell constant, the conductance of the standard solution needs to be
measured. The conductivity of the standard solution is known. Usually, KCl is
used as the standard solution whose conductivity is known at different
temperatures and concentrations. Cell concentration is determined with the help
of Wheatstone bridge.
AB is an
uniform wire, Rx is the variable unknown resistance placed in one
arm of bridge. D is the current detector which determines whether current is
flowing in the circuit or not. The conductivity cell is placed in another arm.
This cell is placed in KCl solution of unknown resistance. D is the current
detector which determines whether current is flowing in the circuit or not.
Wheatstone bridge works on the principle of null deflection, i.e. the ratio of
their resistances is equal, and no current flows through the circuit. F is the
moving point. It is moved in a way that no current flows in the circuit. C is
the point across AB such that resistance across arm where the conductivity cell
is placed will be equal to the resistance across arm of Rx so that
no current flows through this circuit.
Now,
according to Wheatstone bridge principle
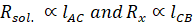
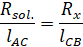
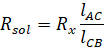
From the
above formulae, resistance of KCl can be calculated by measuring the value of
lengths of AC and BC as Rx. Also, cell constant is given by,
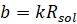
pH
In pH ‘p’
stands for potenz meaning strength. It refers to the concentration of the
hydrogen ions in a solution. pH is defined as the negative logarithm of H+ ion
concentration.
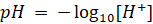
This equation
is used to determine pH when H+ ion is known. The pH scale is
logarithmic and shows the solution’s concentration of hydrogen ions inversely.
More specifically, the pH of the solution is the negative logarithm to the base
10 of its hydrogen ion concentration in moles per litre. A pH scale is a tool for
measuring acids and bases. The scale ranges from 0-14. Litmus paper is an
indicator used to tell if a substance is an acid or a base. The colour of the
paper matches up with the numbers on the pH scale to indicate what kind of
substance is being tested.
If [H+]
> 10–7 , pH is less than 7 and the solution is acidic.
If [H+]
= 10–7 , pH is 7 and the solution is neutral.
If [H+]
< 10–7 , pH is more than 7 and the solution is basic.
pOH
Just as pH,
pOH is defined as negative logarithm to the base 10 of [OH–] pOH is
the measure of acidity or alkalinity of a solution by determining the
concentration of OH− ions.
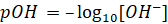
ü If the pOH
value is less than 7, the solution is basic.
ü If the pOH
value is equivalent to 7, the solution is neutral.
ü If the pOH
value is more than 7, the solution is acidic.
Consider the
dissociation of water,
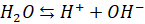
The
dissociation constant Kw would be equivalent to
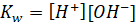
Where,
Kw
is dissociation constant
[H+]
is hydrogen ion concentration
[OH–]
is hydroxide ion concentration
Taking
negative log on both sides
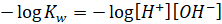
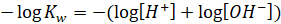
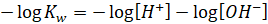
As we know,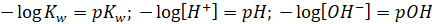 
If, 
then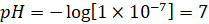 
Similarly,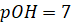 
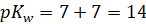
pH
of Acids and Bases
The pH of a
solution varies from 0 to 14.
ü Solutions
having a value of pH ranging from 0 to 7 on the pH scale are termed as acidic
and the value of pH ranging from 7 to 14 on pH scale are known as basic
solutions.
ü Solutions
having the value of pH equal to 7 on pH scale are known as neutral solutions.
ü Solutions
having the value of pH equal to 0 are known to be strongly acidic solutions.
Further, the acidity decreases as the value of pH increases from 0 to 7
whereas, solutions with the value of pH equal to 14 are termed as strongly
basic solutions.
ü The basicity
decreases as the value of pH decreases from 14 to 7. The strength of acids and
bases depends on the number of H+ and OH– ions produced.
Acids furnishing a greater number of H+ ions are known to be strong
acids and vice versa.
Buffer
Solutions
As we know,
solution changes its pH value upon some reactions. But in many cases, we have
to maintain an aqueous solution at constant and specified pH value. For example,
good productivity of crops requires the soil to have proper pH.
Buffer
solutions are used for a wide range of chemical applications. Blood is one
example of a buffer solution found in nature. Human blood has a natural pH of
7.4. Many people experience severe anxiety and suffer from alkalosis. Alkalosis
is a disease in which blood pH is excessively high. The reverse condition is
called acidosis-a blood, pH greater than 7.4
A solution
which has a definite pH and resists any sudden change when a small amount of
strong acid or base is added to it is known as buffer solution or buffer. A
buffer solution is also known as solution of reserve acidity or alkalinity.
ü Characteristics
of buffer solution
ü Stable
concentration of hydrogen ions
ü pH changes
very little with small additions of a strong acid or strong bases.
ü No change in
pH upon dilution
ü It maintains
its pH even when kept for long time.
Types
of Buffers
There are two
types of buffer solution:
Acidic
buffer: A buffer solution that contain a weak
acid and its salt of a strong base. Its pH is below 7. For example, CH3COOH
and CH3COONa, HCOOH and HCOONa, HCOOH and HCOOK etc.
Basic
Buffer: A buffer solution that contain 5a weak base and its salt of
a strong acid. Its pH is above 7. For example, NH4OH and NH4Cl.
Mechanism
of buffering action
For
acidic buffer
Consider pair
of CH3COOH
(acetic acid) and CH3COONa (sodium acelate)
CH3COOH
will be dissociated as
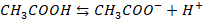
CH3COONa
will be dissociated as
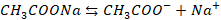
Case
I: Addition of acid: When small quantity of
acid is added to solution, it will dissociate in H+. This H+ ions from
acid combine with CH3COO– ions and produce practically
unionised CH3COOH. This CH3COOH again dissociates but
produce a very small amount of H+ ions.
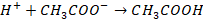
These H+ ions are no
sufficient to change the pH of the solution. The addition of acid is
neutralised by CH3COO– ions. This produce weakly ionised
CH3COOH. The resistance to change in pH of a buffer on addition of
small amount of acid is known as reserve basicity.
Case
II: Addition of base: When small quantity of
base is added to solution, it will dissociate in OH– ions. The OH–
ions from base combines with undissociated acetic acid.
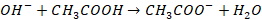
Most of the OH– ions
are consumed by undissociated acetic acid. Therefore, addition of base is
neutralised by acid. The resistance to change in pH of a buffer on addition of
small amount of base is known as reserve acidity.
For
basic buffer
Consider pair
of NH4OH
and NH4Cl.
NH4Cl
is completely ionised in 
and Cl– .
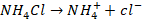
The weak
base, NH4OH is slightly ionised
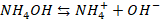
Case
I:
When an acid is added, it forms H+ ions. This ion combines with
undissociated NH4OH.
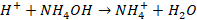
Thus H+ ions
are consumed by NH4OH and pH of the solution remains unchanged. The
addition of an acid is neutralised by NH4OH (base). This buffer
solution has reserve basicity.
Case
II:
When base is added, it forms OH– ions. This ion combines with to form weakly ionized NH4OH
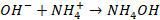
Thus H+
ions are consumed by NH4OH and pH of the solution remains unchanged.
The addition of an acid is neutralised by NH4OH (base). This buffer
solution has reserve basicity.
Preparation
of a buffer solution of desired pH
Acidic
Buffer
Consider an
acid buffer solution, containing a weak acid (HA) and its salt with a strong
base (KOH). The weak acid HA ionises as
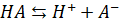
Acid
dissociation constant of HA is given by
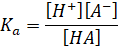
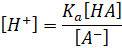
Taking log on
both sides, we have
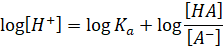
Taking
negative sign on both sides
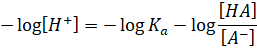
[A-]
= [salt] because the maximum number of A– ions are obtained from the
salt BA
[HA] =
concentration of acid
Also,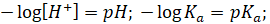 
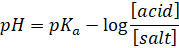
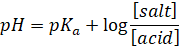
The equation
is the Henderson-Hasselbalch equation, popularly known as the Henderson
equation for acidic buffer.
Basic
Buffer
Consider a
basic buffer obtained by mixing weak base BOH and a salt of weak base and
strong acid BA. The base BOH being weak, dissociates slightly while the salt BA
dissociates completely.
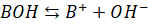
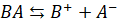
Base
dissociation constant is given by
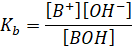
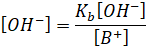
[B+]
= [salt] because
the maximum number of B+ ions are obtained from the salt BA
[BOH] =
concentration of base
Taking log on
both sides, we get
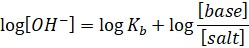
Taking
negative sign on both sides, we have
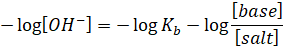
But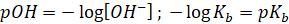 
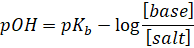
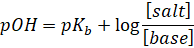
This is
called as Henderson’s equation for basic buffer.
Buffer
capacity
The magnitude
of the buffer action is determined by its capacity. It is defined as the amount
of strong acid or strong base required to produce a change in the pH of the
buffer by one unit.
To prepare an
acidic or basic buffer of desired pH, the acid or base selected should have pKa
or pKb values near to the required pH. The pH of a buffer solution is
determined by the ratio of concentrations of the salt and acid and not by their
amounts. However, the buffer capacity at a given pH does depend upon the actual
concentration.
Reserved
acidity: The property of a buffer to remove the
added OH– ions from its solution with the help of an acid so as to
maintain its pH value constant is called reserved acidity.
Reserved
basicity: The property of a buffer to remove the
added H+ ions from its solution with the help of a base so as to
maintain its pH value constant is called reserved basicity.
Application
of buffer solutions
ü Buffers are
used for biological studies and control of manufacturing processes based on
biological reactions such as brewing industry, manufacture of fungal
anti-biotics etc.
ü Sodium
benzoate acts as a buffer in the preservation of jams and jellies.
ü Buffer
solutions in human blood maintain the pH within the range of 7.35 to 7.45. Any
change of pH in blood from 7.3 to 7 may prove fatal to the person.
ü For growth of
crops, proper pH is necessary.